This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
The corresponding files can be obtained from:
- Jupyter Notebook:
penalty.ipynb - Python script:
penalty.py
Hertzian contact with a rigid indenter using a penalty approach¶
In this numerical tour, we explore the formulation of frictionless contact between a rigid surface (the indenter) and an elastic domain, representing an infinite half-space for the present case. Contact will be solved using a penalty formulation, that is small interpenetration between the solid and the indenter will be authorized. Prerequisites for this tour are the formulation of an linear elasticity problem and the resolution of a general nonlinear variational problem. See for instance:
- https://comet-fenics.readthedocs.io/en/latest/demo/elasticity/2D_elasticity.py.html
- https://fenicsproject.org/olddocs/dolfin/latest/python/demos/hyperelasticity/demo_hyperelasticity.py.html
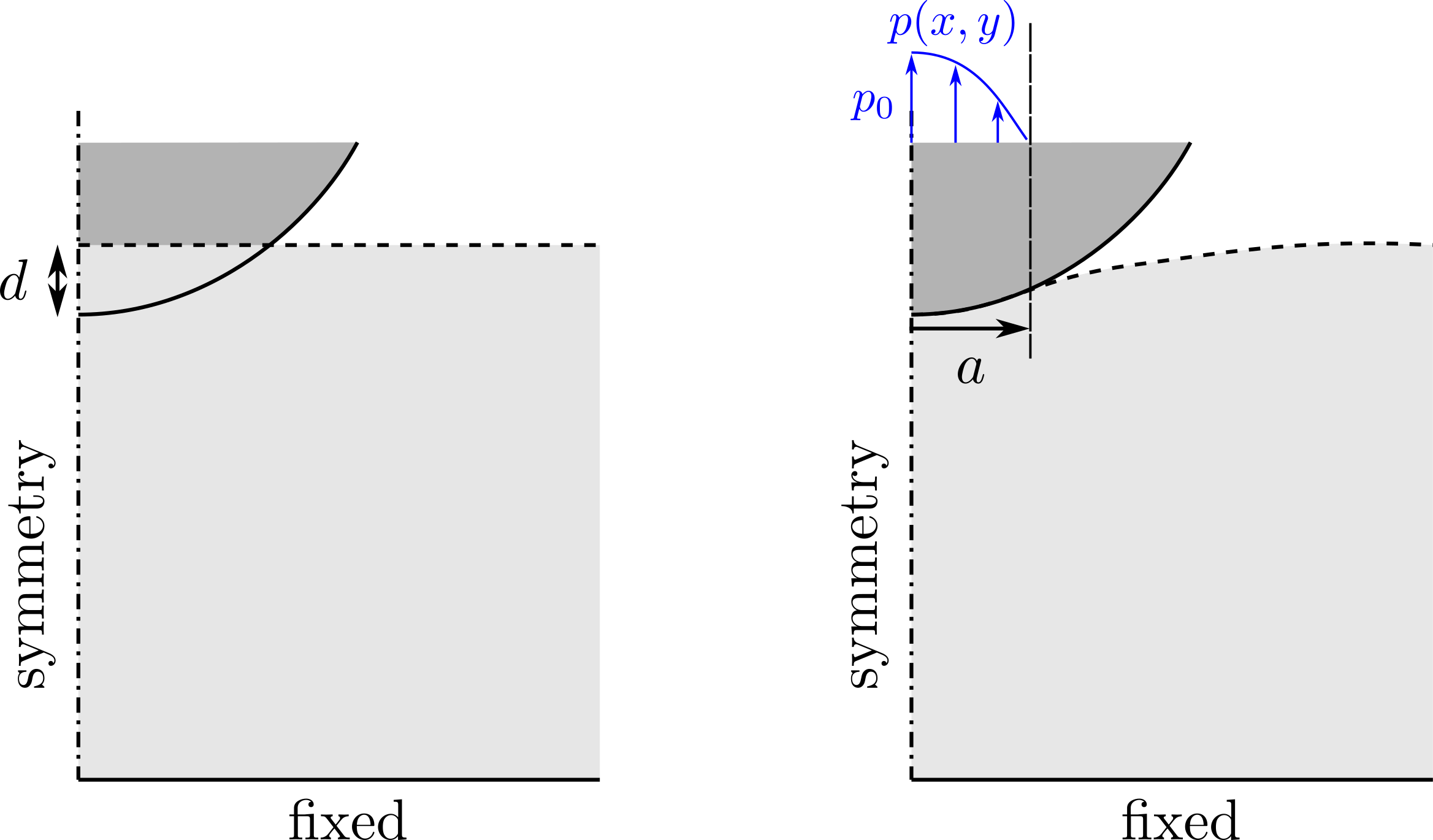
The elastic (isotropic \(E,\nu\)) solid will be represented by a 3D cubic domain of unit dimension and contact will take place on its top surface \(z=0\), centered at \(x=y=0\). Symmetry conditions will be applied on the \(x=0\) and \(y=0\) surfaces whereas the bottom surface \(z=-1\) will be fully fixed. If contact appears on a small region of extent \(a\ll 1\), the problem can then be considered to be a good approximation of contact on a semi-infinite domain.
The rigid indenter will not be explictly modeled (in particular it will not be meshed) but instead its distance with respect to the solid top surface will be given as an Expression. We will also consider that the indenter radius \(R\) is sufficiently large with respect to the contact region characteristic size \(a\) so that the spherical surface can be approximated by a parabola. In this case, the distance between such an indenter and the top surface can be written as:
where \(h_0\) is the initial gap between both surfaces at \(x=y=0\). Obviously, if \(h_0>0\) there is no contact between both surfaces, contact appears only if \(h_0=-d<0\) where \(d\) will be the indenter depth inside the surface. This classical problem admits the following known analytical solution [1,2]:
- the contact area is of circular shape and radius \(a=\sqrt{Rd}\)
- the force exerted by the indenter onto the surface is \(F=\dfrac{4}{3}\dfrac{E}{1-\nu^2}ad\)
- the pressure distribution on the contact region is given by \(p(r) = p_0\sqrt{1-(r/a)^2}\) where \(p_0=3F/(2\pi a^2)\) is the maximal pressure
Contact problem formulation and penalty approach¶
The unilateral contact (Signorini) condition on the top surface \(\Gamma\) writes as:
where \(g=h-u\) is the gap between the obstacle surface and the solid surface and \(p=-\sigma_{zz}\) is the pressure. One of the most simple way to solve approximately this contact condition consists in replacing the previous complementary conditions by the following penalized condition:
where \(\langle x\rangle_+ = (|x|+x)/2\) is the positive part (Mackauley bracket) and \(k\) is a large penalizing stiffness coefficient. With the previous relation, the pressure will be positive but a small negative gap will be authorized.
Implementation¶
First, a unit cubic mesh is defined and some mapping is applied on the mesh nodes in order to refine the element size near the contact area (around \(x=y=z=0\)) and change to a \([0;1]\times [0;1]\times[-1;0]\) domain.
[15]:
from dolfin import *
import numpy as np
N = 30
mesh = UnitCubeMesh.create(N, N, N//2, CellType.Type.hexahedron)
# mesh size is smaller near x=y=0
mesh.coordinates()[:, :2] = mesh.coordinates()[:, :2]**2
# mesh size is smaller near z=0 and mapped to a [-1;0] domain along z
mesh.coordinates()[:, 2] = -mesh.coordinates()[:, 2]**2
The top surface is defined as a SubDomain and corresponding exterior facets are marked as 1. Functions for imposition of Dirichlet BC on other boundaries are also defined.
[16]:
class Top(SubDomain):
def inside(self, x, on_boundary):
return near(x[2], 0.) and on_boundary
def symmetry_x(x, on_boundary):
return near(x[0], 0) and on_boundary
def symmetry_y(x, on_boundary):
return near(x[1], 0) and on_boundary
def bottom(x, on_boundary):
return near(x[2], -1) and on_boundary
# exterior facets MeshFunction
facets = MeshFunction("size_t", mesh, 2)
facets.set_all(0)
Top().mark(facets, 1)
ds = Measure('ds', subdomain_data=facets)
The obstacle shape \(h(x,y)\) is now defined and a small indentation depth \(d\) is considered. Standard function spaces are then defined for the problem formulation and output field exports. In particular, gap and pressure will be saved later. Finally, the DirichletBC are defined.
[17]:
R = 0.5
d = 0.02
obstacle = Expression("-d+(pow(x[0],2)+pow(x[1], 2))/2/R", d=d, R=R, degree=2)
V = VectorFunctionSpace(mesh, "CG", 1)
V2 = FunctionSpace(mesh, "CG", 1)
V0 = FunctionSpace(mesh, "DG", 0)
u = Function(V, name="Displacement")
du = TrialFunction(V)
u_ = TestFunction(V)
gap = Function(V2, name="Gap")
p = Function(V0, name="Contact pressure")
bc =[DirichletBC(V, Constant((0., 0., 0.)), bottom),
DirichletBC(V.sub(0), Constant(0.), symmetry_x),
DirichletBC(V.sub(1), Constant(0.), symmetry_y)]
The elastic constants and functions for formulating the weak form are defined. A penalization stiffness pen is introduced and the penalized weak form
is defined. The corresponding Jacobian J is also computed using automatic differentiation.
[18]:
E = Constant(10.)
nu = Constant(0.3)
mu = E/2/(1+nu)
lmbda = E*nu/(1+nu)/(1-2*nu)
def eps(v):
return sym(grad(v))
def sigma(v):
return lmbda*tr(eps(v))*Identity(3) + 2.0*mu*eps(v)
def ppos(x):
return (x+abs(x))/2.
pen = Constant(1e4)
form = inner(sigma(u), eps(u_))*dx + pen*dot(u_[2], ppos(u[2]-obstacle))*ds(1)
J = derivative(form, u, du)
A non-linear solver is now defined for solving the previous problem. Due to the 3D nature of the problem with a significant number of elements, an iterative Conjugate-Gradient solver is chosen for the linear solver inside the Newton iterations. Note that choosing a large penalization parameter deteriorates the problem conditioning so that solving time will drastically increase and can eventually fail.
[19]:
problem = NonlinearVariationalProblem(form, u, bc, J=J)
solver = NonlinearVariationalSolver(problem)
solver.parameters["newton_solver"]["linear_solver"] = "cg"
solver.parameters["newton_solver"]["preconditioner"] = "ilu"
solver.solve()
[19]:
(8, True)
As post-processing, the gap is computed (here on the whole mesh) as well as the pressure. The maximal pressure and the total force resultant (note the factor 4 due to the symmetry of the problem) are compared with respect to the analytical solution. Finally, XDMF output is performed.
[20]:
p.assign(-project(sigma(u)[2, 2], V0))
gap.assign(project(obstacle-u[2], V2))
a = sqrt(R*d)
F = 4/3.*float(E)/(1-float(nu)**2)*a*d
p0 = 3*F/(2*pi*a**2)
print("Maximum pressure FE: {0:8.5f} Hertz: {1:8.5f}".format(max(np.abs(p.vector().get_local())), p0))
print("Applied force FE: {0:8.5f} Hertz: {1:8.5f}".format(4*assemble(p*ds(1)), F))
file_results = XDMFFile("contact_penalty_results.xdmf")
file_results.parameters["flush_output"] = True
file_results.parameters["functions_share_mesh"] = True
file_results.write(u, 0.)
file_results.write(gap, 0.)
file_results.write(p, 0.)
Maximum pressure FE: 1.42763 Hertz: 1.39916
Applied force FE: 0.03206 Hertz: 0.02930
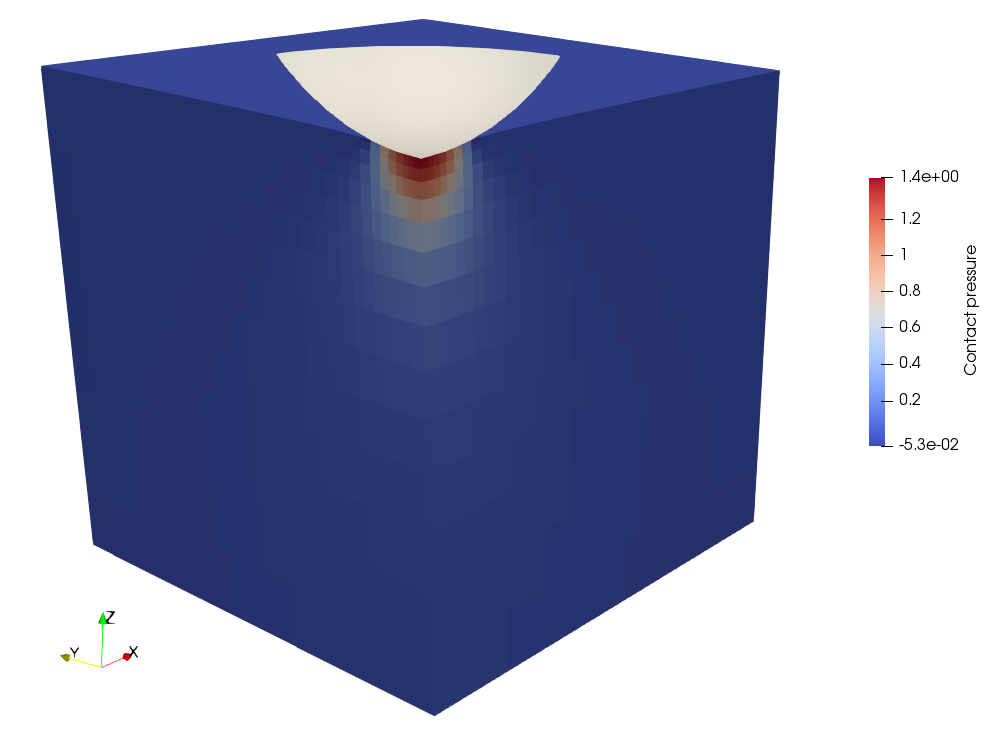
Maximum pressure over the contact surface and total applied force by the indenter are computed and compared against the analytical solution. Comparison between both solutions shows good agreement although the quality of the results is quite dependent on the chosen penalty sitffness. Here is what the solution looks like.
References¶
[1] K.L., Johnson, Contact Mechanics, Cambridge University Press, 1987
[2] S.P. Timoshenko, J.N. Goodier. Theory of Elasticity, MacGraw Hill International Book, 1982
[ ]: